K-means Clustering
Classification is the technique where we attempt to group data based on their similarities and thereby to categorize them. For example, if we wanted to categorize fresh produce as either vegetable or fruit, we could compare attributes such as sweetness, crunchiness, etc.. Whereas an apple would be sweet and crunchy, an onion would not be. Because of these unique differences we can differentiate one group (e.g. vegetables) from the other (e.g. fruits). With this in mind today we explore one of the most common approaches K-means Clustering with SciKit-Learn.
Classifying Cars with K-means Clustering
As an illustration we will show a simple example regarding cars. Chiefly, given several specifications of a car how can we classify them as either a SUV, Convertible, or a Sedan. Even though this may sound easy for a human, for a computer this will depend on being able to group cars with similar traits together.
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
carlist = pd.read_csv("CarList.csv")
carlist.head()
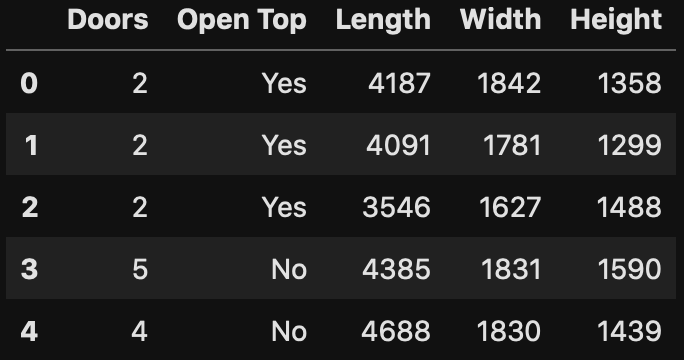
Equally important convert our categorical data into a numerical format. Furthermore, remember to normalize our data before applying any analysis. Accordingly one of our earlier posts provide you with a quick how to normalize your data.
# Normalize our data
carlist = (carlist - carlist.mean())/carlist.std()
carlist.head()
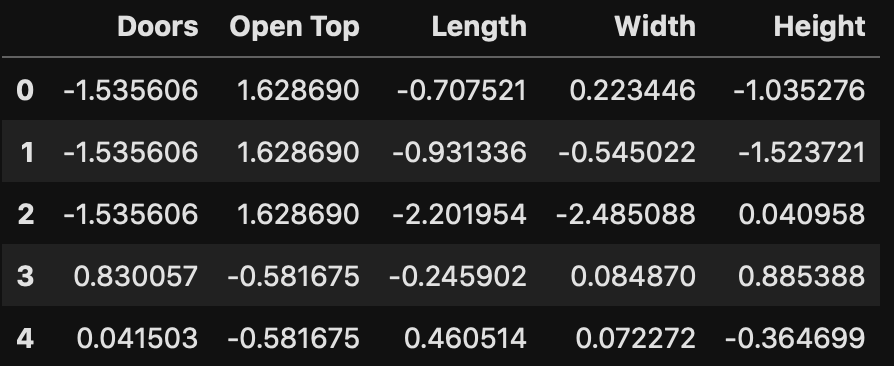
As shown above we have details about how many doors there are, whether the top is open, and general dimensions of the car. Additionally you may also realize that all our data are numerical. To be sure, we run a simple check.
carlist.dtypes
Doors float64
Open Top float64
Length float64
Width float64
Height float64
dtype: objectBuilding a model with K-means Clustering
Since our data is clean we will next proceed to build a data model for K-means Clustering. Generally a data model is able to take input data and generate an output or prediction based on a set of algorithms. At the present time we will not go deep into the code and math behind the algorithm. Instead we will try to describe what is happening in 6 steps.
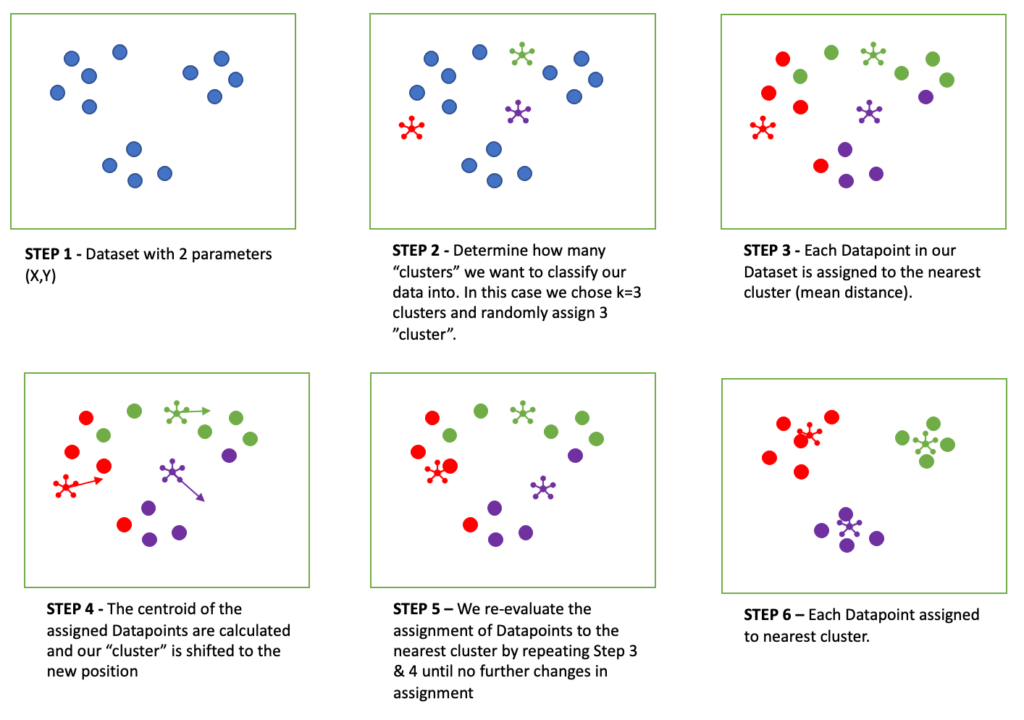
In order to create our model, we will use Scikit-learn with a simple line of code. Meanwhile as we are attempting to classify our cars into 3 categories, we want to define a model with 3 clusters.
model = KMeans(n_clusters=3)
Fitting our data to K-means clustering model
At this point we have defined our model. Accordingly the next step is to feed our model with our data. Hence our model would be able to run through the K-means clustering algorithm.
model.fit(carlist)
KMeans(n_clusters=3)Evaluating our model results
Finally with our model trained we can proceed to evaluate the results of our classification. For that reason we can run a single command to see our results
print(model.labels_)
[0 0 0 1 2 2 1 2 1 1 2 1 0 1 1 2 1 2 2]Obviously we can see that each value corresponds to the category in our original car list. Furthermore to better evaluate our results, we compare this with the true value of our dataset. This process is commonly referred to as validation – the act of comparing predicted results with known results.
carlist['Prediction']=model.labels_
# Retrieving the true values of the Car and Label
pd.concat([fullcarlist['Car'],fullcarlist['Label'],carlist['Prediction']], axis=1)
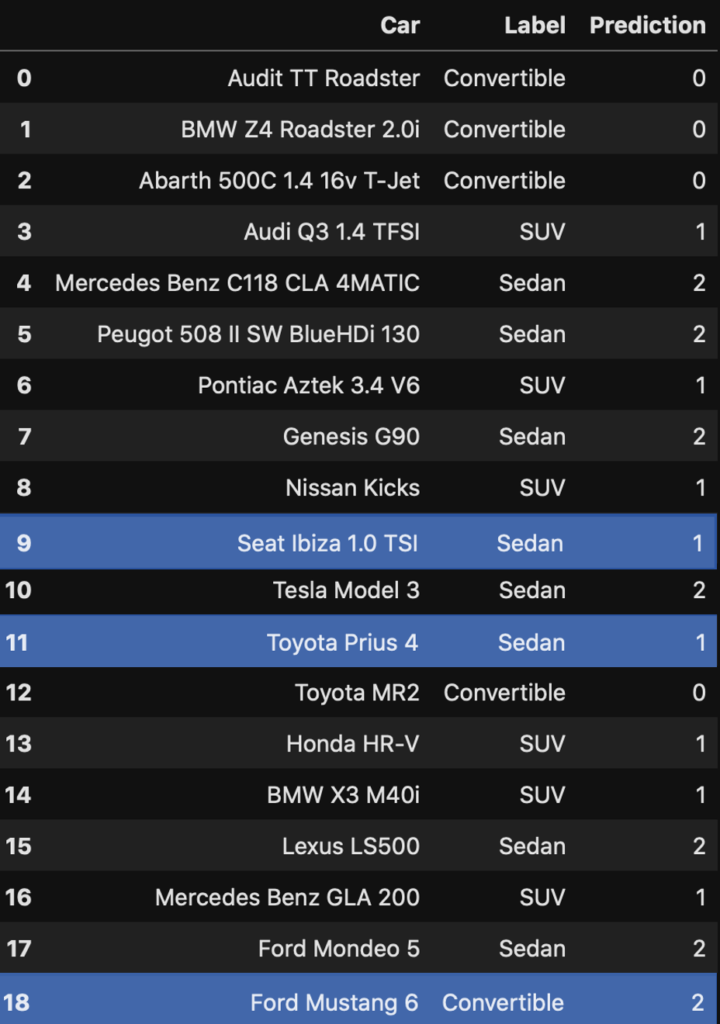
As can be seen, our K-means clustering model was correct 84.2% of the time (16 of 19) with three cars incorrectly classified.
Summary
In short today we have seen how with only a few lines of code we can use Scikit-learn to perform K-means clustering. As with any mathematical model, the accuracy of our classification will depend highly on our data. Undoubtedly with more data points, the chances of a validation accuracy can be achieved. Likewise it can be the traits used were not telling enough to accurately tell between a SUV, Sedan, or Convertible. Nonetheless we hope we have been able to briefly explain the concept of K-means clustering and you would be able to apply this in your analysis. Moreover there are many practical applications of classification such as customer segmentation, determining if a bank loan should be granted, etc..



